Describe the General Properties of Rotations
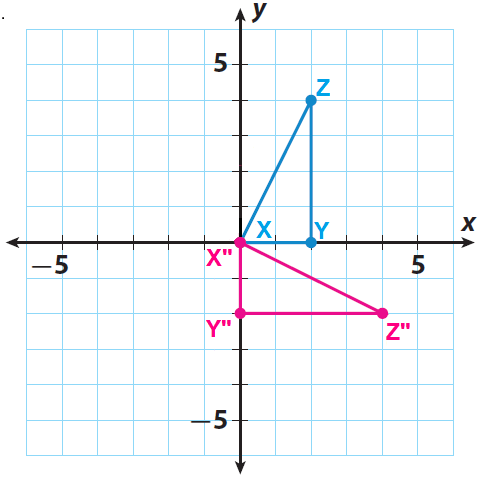
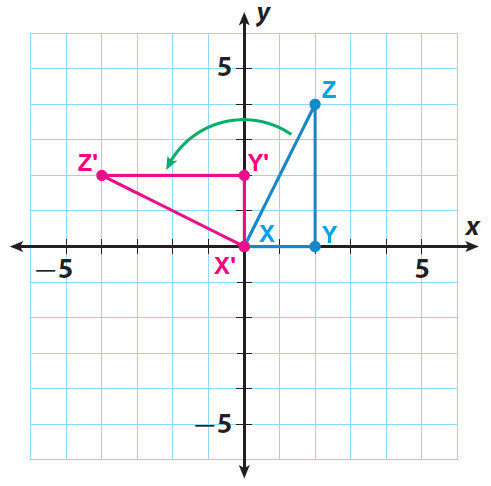
A rotation maps a line to a line a ray to a ray a segment to a segment and an angle to an angle. Rotations preserve size rotations of 360 map a figure to itself and lines connecting the center of rotation to the pre-image and the corresponding point on the image.

Geometric Rotations Worksheets Discovery Based Learning Middle School Math Writing Linear Equations
This approach utilizes the.

. R1 A rotation maps a line to a line a ray to a ray a segment to a segment and an angle to an angle. In this last concept you will look at the properties of rotations. The composition of two reflections about intersecting lines produces a rotation.
Cut out your tracing. Each point and each image is the same distance from the centre of rotation. Up to 24 cash back Properties of Rotations Use trapezoid TRAP to investigate the properties of rotations.
Complete the mathematical statements for these two properties of rigid body transformations above. A rotation preserves lengths of segments. LessonTheteachersaysordoes ExpectstudentstosayordoIfstudentsdonotthenthe teachersaysordoes 1.
The following are the three basic properties of rotations. As a rotation matrix is always an orthogonal matrix the transpose will be equal to the inverse of the matrix. However the orientation is not preserved.
A rotation is an isometric transformation that turns every point of a figure through a specified angle and direction about a fixed point. Up to 24 cash back Properties of rotation. Its center of rotation is the intersection of the lines.
Rotations are rigid transformations which means they preserve the size length shape and angle measures of the figure. A rotation matrix will always be a square matrix. It preserves size corresponding length of each side remains same and shape corresponding interior angles remains same of figure.
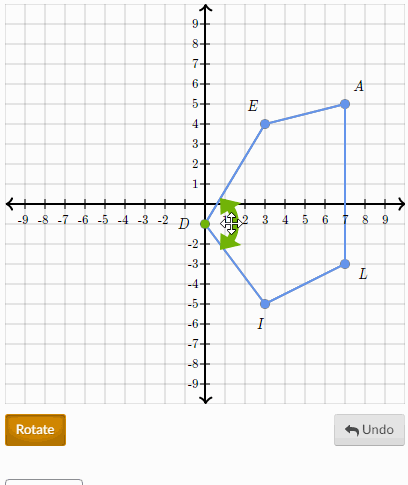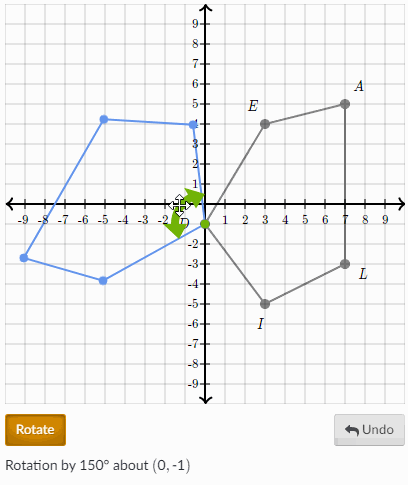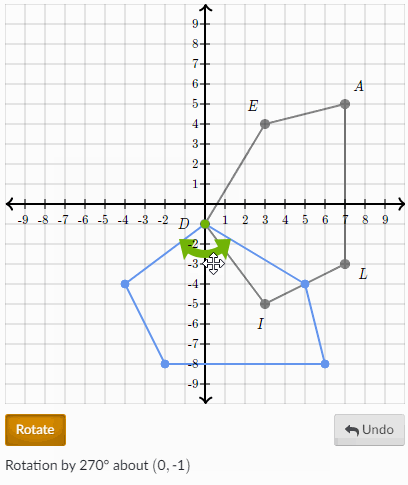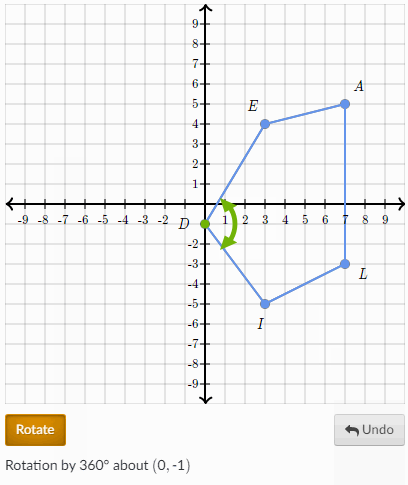
Direction clockwise CW or counterclockwise CCW Angle in degrees. This is the centre of rotation. Trace the trapezoid onto a piece of paper.
Rotations are rigid transformations which means they preserve the size length shape and angle measures of the figure. Multiplication of rotation matrices will result in a rotation matrix. As you learned earlier rotations involve turns or spins of a preimage to form a rotated image.
The line segments connecting corresponding vertices are not parallel. Line segments connecting the center of rotation to a point on the pre-image and the corresponding point on the image have equal length. Line segments connecting the center of rotation to a point on the pre-image and the corresponding point on the image have equal length.
Basic Properties of Rotations. However the orientation is not preserved. However the orientation is not preserved.
Rotations are rigid transformations which means they preserve the size length shape and angle measures of the figure. The properties of rotation are. There is only one invariant point.
To describe a rotation you need three things. Then use the axes to help rotate. A rotation is a rigid transformation sometimes called an isometric transformation that moves every point of the pre-image through an angle of rotation about the center of rotation to create an image.
Line segments connecting the center of rotation to a point on the pre-image and the. In general rigid body transformations consist of rotation and translation as is depicted in Fig. The angle of rotation is equal to twice the measure of the angle formed by the two lines.
Every point moves through the same angle around the centre of rotation. A rotation matrix when applied as an operator via matrix multiplication is a valid rigid body transformation. Center point of rotation turn about what point.
The line segments connecting corresponding vertices are not parallel. R3 A rotation preserves degrees of angles. Include the portion of the x- and y-axes bordering the third quadrant.
Place your trapezoid and axes on top of those in the figure. The determinant of a rotation matrix will always be equal to 1. The Properties of a Rotation Concept Content.
An analytical approach is presented for studying the convergence of the general Jacobi method applied to diagonalizing the second-rank tensors that describe the optical properties of a medium subjected to an external field. A rotation is a rigid transformation that forms image of a shape with same shape and size by rotating it about the the center of rotation. Rotations result when an image and its rotated image have the same shape but the rotated image may be turned in different directions.
R2 A rotation preserves lengths of segments. In order to perform a rotation of an object a point of rotation angle of rotation and. A rotation preserves measures of angles.
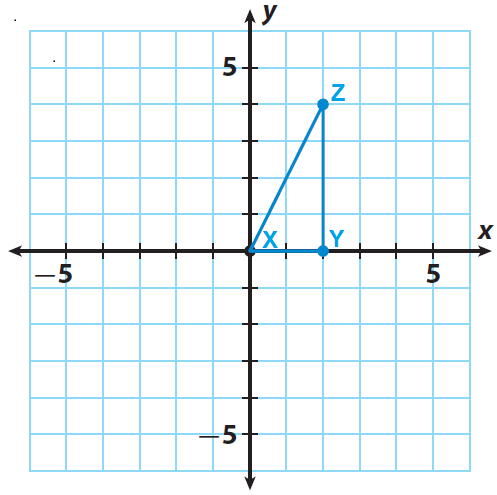
Comments
Post a Comment